Noise is almost as interesting as signals. In fact, noise is a component inherent in all physical signals, even those that have yet to pass through a channel. That will include (at least) phase noise, several tabs down.

Now, before going any further, consider the following statement:

Noise is an element or aggregation of elements affecting a measurement which is (or are, in the case of mulitple, aggregate elements) independent of a desired signal which also resides, partially or completely, in the "space" accessible to the measuring device.

The desired signal in the above is an abstraction, a "noiseless thing" which might be called a perfect embodiment of some information. A purely mathematical entity. The sender's intention, wrapped up as a symbol, not yet a physical signal. This is not the usual "desired signal" in a radio bandwidth coming out of a rig speaker, or interface to a PC.

The physical "space" above consists of measurable time and bandwidth. It is a law of physics that the product of these two, the time-bandwidth or TB product, cannot be less than a lower limit, even in theory (let alone implementation). This is a statement of the uncertainty principle. (Adopted from Heisenburg's quantum uncertainty, now applying to any system from atomic to macro structures of electrical circuits, etc.) For many systems, including the ordinary filters, amplifiers and detectors in our radios, T(sec, or Hz^-1) x B(Hz) > 2.4, or else you cannot communicate reliably! It is a necessary, though not sufficient, part of the capacity theorem in information theory.

Noise, particularly from LF to VHF, can originate from "natural" sources like lightning (QRN), manmade sources not of a communications nature like motors (technically QRM, but often given QRN status if not easily distinguished from natural static), and finally (though hardly least in many cases) any undesired signal (QRM, or interference being the more precise word) overlapping your desired signal (regardless of how it got there). All this is noise, in your bandwidth of interest and across your observation time of a desired signal, or any piece thereof.

Now we are set to proceed.

 

 

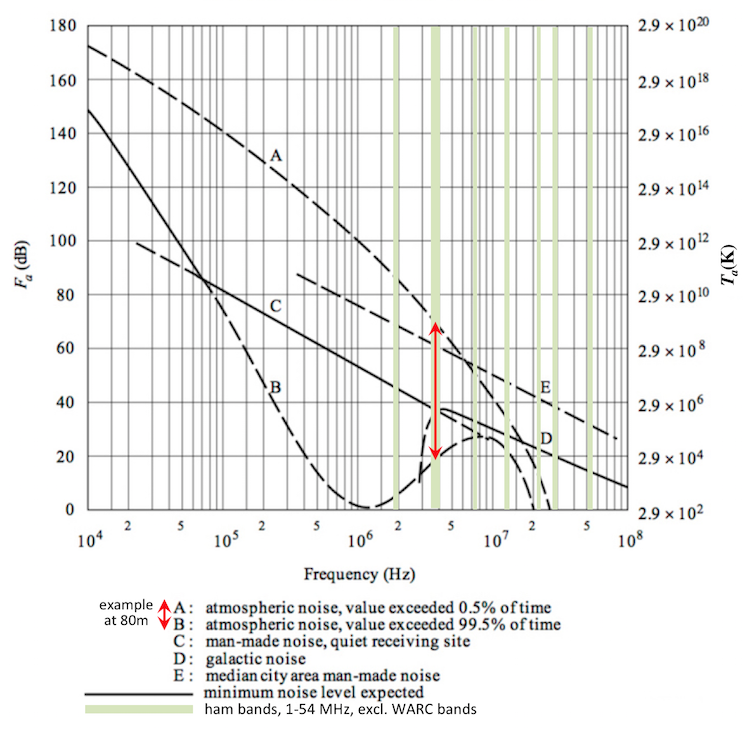
Noise factor is a good lauching point, because it is easy to think about and quantify. It is about thermal noise. And so, it uses a concept called the "system temperature" of a radio communications link. This link comprises everything up to the key step of detecting a signal and replacing it with either a number (or series of them) or else a human sensible quantity like sound. Once we're to detected information, even if it is corrupted by errors or distortions (as the very result of thermal and other physical noise), we are then beyond the concept of noise factor - physical system temperature can no longer bother us (though we are stuck with its effects on the detector).

Noise factor can be an oversimplification when other (important) imperfections of an otherwise "ideal channel" reduce the reliability of communication, imperfections like impulsive noise or distortion. Nevertheless, at UHF and below, noise factor is a fundamental aspect in what is called the link budget.

Back to ham radio, particularly up to VHF. The ITU made longterm, averaged measurements of thermal, and thermal-like noise for use as references (e.g., in proposals to use international radio spectrum). That's the next tab. "Thermal-like" encompasses a world of noise sources that can be represented by the temperature of a black body.

Noise factor follows the black body radiation intensity curve (a Rayleigh random variable (r.v.) power curve, up to the famous ultraviolet catastrophe, where it gives way to Planck's quantum resolution). [A Rayleigh pdf/cdf is just the pdf/cdf of the square of a Gaussian r.v., as in, say, microvolts at your antenna terminals.] Hams haven't overly concerned themselves with ultraviolet-and-beyond communications, but it's probably just a matter of time. Hams already routinely do optical laser communications which border on their intrinsic noise breaking free of Rayleigh, which goes on continuously forever up in frequency ... that catastrophe. These hams are already in the world of quantum communications.

But back to noise factor, denoted as F. F is just the numeric (antilog) value of the logarithmic (dB) noise figure F (italicized to make this distinction). It's easier to work with F when discussing what it means. But it's a lot easier to say "dB" when conveying a noise situation to someone else on the other end of a radio link.

Noise factor simplifies the whole thing by referring to a "standard candle" of noise. That standard in radio is a blackbody noise at 290 Kelvin (or about room temperature) located right at your antenna terminals, or if you are a radio manufacturer, right at your radio's external (e.g., coax) connector. There are simple rules for "ganging up" antenna, transmission line and radio F's into an overall F, which we won't bother with here. This aggregate is the system noise factor. At HF, it all starts with the environment of a good (read, very negligible F) antenna. This is what the ITU graph on the next tab is all about, up to 100MHz, that is.

So here is noise factor F in all its glory. Start with effective noise temperature at any point in an electrical system Te = To (F-1), To = 290K by convention. Solving, we get F = (Te/To)+1, or if you prefer dB, F = 10 log10((Te/To)+1)dB, because this is all about power, not scalars like voltage, even though F (and F) is dimensionless.

You may not find that useful because you don't have the right thermometer to capture Te, but maybe you have a power meter. For thermal power, N(Watts) = kTB, where T is temperature, k is Boltzmann's constant and B is bandwidth. There's that TB product again, and there are places on the Rayleigh curve of Gaussian power where you you can't communicate! In practice, it's where we try to exceed (or even get very near) capacity C, which has never been demonstrated and, in theory, never will be (despite a quacky claim or two in the recent past). It's also where B approaches 0 Hz very closely, since we don't have an infinite amount of time T to both set up the initial conditions and pull out a baud from a filter. Fortunately, we can communicate most everywhere else so long as the SNR is high enough and the modulation and coding are "strong" enough.

If you want a number for kTB, it's easier to add things in dB, i.e. P(dBW) = k(in dB) + T(dBK(elvin)) + B(dBHz), where k = -228.6dB(W/(K-Hz)), and deal in F(dB). This is how we get around using the inconvenient SI unit Joules. So for a radio and antenna, both at room temperature (To = 10 log10(290K) = 24.6dBK, with a perfect frontend and zero environmental noise (never happens!), Te = 24.6dBK also, and at our typical ham radio reference bandwidth B = 10 log10(2800Hz) = 34.5dBHz, then N = -169.5dBW = -139.5dBm. Can we never do better than this? Yes, we can cool the frontend and antenna (somehow) down to nearly zero, i.e. let it be 1 Kelvin, hard to do any better (even with the resources of a nation state) and this is a sort of universal lower limit. If so, then To = 10 log10(1K) = 0dBK, and we do 24.6dB better, or N = -163.1dBm. But a ham will never get that 1.0K system temp! Possibly not even the best lab or radiotelescope.

If you want to see ITU's typical noise power at some frequency (below about 100MHz) in some bandwidth (say our ham reference 2.8kHz) at your antenna terminals, you use the graph in the next tab, and deal with that pesky 290K lowest value on the graph by treating it as zero, i.e. by just letting F-1 -> F for most all environments of practical interest, and calculate N = Ta + k + B (all in dB) = 10 log10(To (F-1)) + k + B -> N ~ To + Fa + k + B = (Fa - 139.5)dBm. In the middle of the 80m curve (quiet receiving spot, curve C), this is -99.5 dBm. At 50 ohms real, this is 75uV rms, so that 1.5uV rig sensitivity spec (at 10dB (S+N)/N, no preamp) is not of much use!

 

 

And Now, A Word from Our Atmosphere!

Setting aside the threat to your rig (mostly from static buildup rather than strikes), lightning captivates your HF receiver in an otherwise nice, quiet QTH.

The ITU drew a graph way back, pretty much* holding its own today. Fa below is the "noise figure of the entire transmission channel," including any antenna (a) losses, at the antenna terminal output to your rig. Translated to the receive electronics, Fa presumes the antenna termination is matched to the rig input impedance. For an explanation of F in general, see the previous tab.

The graph breaks up a total Fa(tot) into three additive, constituent parts A-to-B, C or E, and D. Reading the legend will make that plain. That span between curves A and B is mostly** lightning, striking somewhere, propagating to you as all direct paths and the ionosphere allow, from exceedence probability 99.5% (almost always) to 0.5% (almost never).

One thing to note, for the red arrow at 80m, is the huge range of atmospheric noise conditions, about 50 dB! Even at 20m, it is almost a 30dB "range of experience" across all the times you might ever look. At 6dB power per S-unit (see that tab), you see 80m background noise spanning over 8 S-units, and at 40m over 5 S-units. No wonder "band conditions" are such a big deal. The situation for 160m boggles the mind.

 

Lightning is more important than man-made noise at many rural and many suburban QTHs from 2200m to 20m. In stormy weather, watch big crashes from local strikes across your rig's waterfall, but that rolling, unrelenting noise floor, even on nice, blue sky days, is mostly lightning from all directions, much of it originating at sea! In thunderstorm season, local (even beyond 50km) strikes show up as wideband (WB) blasts that are fortunately each short (often made up of many FFT-indistinguishable successive strokes, each less than a millisec). There are cloud-to-cloud and cloud-to-ground strikes, the former perhaps predominant. There are rare monsters of rapid fire "circuits" up to seconds. Nevertheless, add up all the independent strikes over millions of square km, and you get something resembling a "floor" of WB noise. The floor varies momentarily enough to aid digital noise reduction algorithms (which also exploit desired signal transients). When a band is up, lightning noise arrives from DX zones thousands of km away.

 

One of the reasons 10m can be magical when the F layers are up to it, is that it's so relatively low in atmospheric noise. Low power goes! We used to chuckle about hearing the Peruvian taxicabs in Arizona when 10 was up.

 

* It's yet another sinister aspect of global warming that "atmospheric" noise is not going away. Rather, it's trending up.

 

** Mostly, because any noise of terrestrial origin propagating via the "atmosphere" (which includes the ionosphere) is in this statistic. And this includes all non-local (non-direct-path) man-made noise. So listening on an "unoccupied" frequency and noting a random noise with the RF and AF gains up high enough, one is hearing lightning, yes, but also the total sum of all man-made noise that has managed to skip to the receiving antenna. And that includes other hams below Q1 readability, city and industrial noise from afar. But it does not include just anything that radiates from the sky downward. That last adds galactic sources, mostly other stars, and also the Sun. These are not atmospheric noises. The Sun is a special case, worth a textbook of its own, but the "quiet Sun" (meaning no large solar flares and their CMEs, etc.) does not compete with lightning below about 30 MHz, most especially because antennas at these HF and lower frequencies have such huge beamwidths that they do not raise the 1M+ degree Kelvin temperature of the Sun's corona, which spans little more than the 1/2 degree width of the Sun's photosphere (try to get that beamwidth at any frequency lower than 10 GHz or so!). The Sun is usually a non-factor with respect to noise for ham antennas using HF under quiet conditions, ignoring infrequent solar storms. It is, however, anything but a non-factor with respect to ionsopheric propagation of man-made signals! A different topic.

Finally, one exceedingly unusual phenomenon can affect LF-HF propagation profoundly. It is the gamma ray burst (GRB) from distant sources, usually outside our Milky Way galaxy. One, GRB221009A, occurred recently, from 2.4 BLy (that's billion) away that wiped out essentially all LF-HF propagation (on at least one side of the planet) for more than 10 minutes. That's worse than the daytime Sun. MUF < 10kHz maybe. Good thing it's likely rarer than the lifetime of any civilization to occur within our galaxy, which would be more than a mere "HF event" for hams, and everyone else.

 

 

This tab will not (yet) try to touch mathematics There are so many great texts that do exactly this, and no possibility of improving on them viz a viz the math in a short page like this. That said ...

The first tab stated that noise is independent of signal. This has huge implications, considered in the Distortions tab.

Noise in radio can be any disturbance of the measurement of an "ideal," if you will (i.e., a perfectly formed and sent), and often shortest, information-bearing signal symbol or sample of a signal, which did not originate from the sender (or transmit system). Noise is almost completely external to a well-implemented transmitter (although even transmitters have noise figures, but usually not large enough to be interesting in ham radio). But not to the receiver!

Now, a textbook could be (and has been, many times) written on signals, and we won't go there here. However, a brief blurb below suggests the turf.*

Noise is most generally additive (to the signal), linearly or even nonlinearly (imagine stretching or shrinking a fixed sent bandwidth). At HF in CW, SSB or higher rate "digital" (including RTTY, which is basically an FSK), we think mainly about simple, additive noise, as featured in that earlier ITU graph tab. This is true, "normally," up to a couple hundred MHz.

Hams and pros alike think of memoryless additive white Gaussian noise (AWGN) as a go-to "random-most" noise in amplitude and phase. This is the fault of the Central Limit Theorem (CLT), which shouldn't be presumed willy-nilly. For example, HF atmospheric noise in that ITU graph can be anything but memoryless or Gaussian over short periods of time, although it's frequently white over the small bandwidths of interest in HF hamdom. Nevertheless, memoryless AWGN is a convenient go-to model in the absence of actual data about a reception situation. Noise with memory is another thing, mostly considered only in digital signaling these days.

At great risk of BS by way of over-compressing a subject, Gaussian noise processes are stationary in the sense that they have the same statistics of amplitude and phase (together yielding a noise spectrum) at any point in time. The classic example is the voltage across a resistor (in, say, a voltage source circuit) at some temperature T. Thermal noise is classically Gaussian! But what if the noise process is not the same at any point in time? Then you have a so-called point process, which if independent in its noise characteristics (e.g., how high, and with what waveshape) at any given time, is a Poisson process. The classic example is shot noise, which looks like, well, shots of (mathematical) energy arriving in a random sequence. This may be a "random-most" noise in time, as opposed to amplitude. If most of your HF noise is due to nearby thunderstorms, it could be argued that your radio channel is shot noise-limited in SNR, not thermal noise-limited. But if the HF noise is all very far away and adds up in great numbers of "shots," we're back to Gaussian via the CLT. So, alas, as far as HF noise goes, it depends! Another case of shot noise is in vacuum tubes, since electrons traveling from cathode to anode don't do so smoothly, but rather in shots. This could matter for higher bandwidth electronics, but hams don't generally use that, and there is little discussion at HF radio frequencies of shot noise. But it's good to know that it exists.

Now again risking critique from the peanut gallery, (relatively) wideband signal fading is, at least at HF, generally not "noise." The fading is not inherent in the transmitted signal, so why is this so? It is because, at least at HF, slow fading is due to organized ionospheric "shifting" of layers of (differing) electron densities. This shifting is not, strictly speaking, shortterm random in nature. It is a process of ionopsheric state change that is almost predictable once it starts moving, up or down. In fact, so-called linear predictive models (and equalizers) can be employed to counter such shifting to some extent. Your receiver's "fast" AGC setting is a crude example. More sophisticated software methods also exist.

Slow fading affects SNR if the noise is not fading (at least as much)! This is to say, the sort of fading that's on a "long scale" of time duration, i.e. across chunks of information, is basically QSB. It results from refractive angles in ionophere layers, additive multipath propagation within and between layers, and also absorptions of various kinds. The absorption most contended with at HF is "thick" D-Layer ionization, a mostly daytime thing that effectively eats up part or all of the signal. This D absorption is the thing that changes fast across the so-called "grey-line," or solar terminator of the Earth. It may not even get through to outer space at any useful level anywhere! Above HF all this differs, and is out of scope for this tab.

However, fading on the shortest scale, i.e. actually a "fading inside of" individual symbols in digital transmissions, starts to look like noise again in this "shortest information symbol" bandwidth. But that's for another discussion on channel coherence time and coherence bandwidth. Again, usually associated with higher rates well above HF.

A little aside. In ionospheric "refraction," aka hop (skip is what's under a hop!), there is something called frequency-selective fading. It becomes interesting when it's of fairly narrow "fade bandwidth" versus a signal's bandwidth. While fundamentally a fading effect, vice an independently-sourced noise effect, this fading can distort signals, sometimes even within a 3 kHz SSB signal's width. You could call distortion noise if and when it continuously varies as you listen to short syllables.

Speaking of hop, you can get multiple, competing refractions off different layers of the ionosphere, say on both F1 and F2 during transitions to local evening time. This means that you can be receiving two versions of a sent signal, one more time-delayed than the other, and if one is very dominant power-wise then the weaker version is most definely a sort of noise. This is also called multipath propagation, the same basic thing as occurs in VHF/UHF land mobile radio in the presence of structures or even very nearby mountains. When you can't put multipath signal fragments back together again, as you can using spread spectrum into a Rake receiver, then you've got both loss and noise, bad news. US hams can't use spread spectrum below 222MHz.

Radio noise may also be quantitatively described as a probability distribution of the coherence properties of a signal baud (in phase and/or time), but also, sort of secondarily, as very rapid absorptions of signal power by rain and atmospheric atoms at super high frequencies (3-30 GHz) and above. These SHF+ absorptions are, again, really multipath conditions, but so dense and concentrated that it's better described as "scattering," appearing as a combination of power fluctuation, along with phase fluctuation (or time delay noise on a very short scale). These are called scintillations. At frequencies from VHF to lower UHF, the ionosphere can exhibit such behavior near the equator (or more accurately, near the geomagnetic equator) and the (geomagnetic) poles. Again, an involved subject that can bedevil satellite communications at certain times and places, especially near 300 MHz.

To wrap up, well-read hams know that any signal, transmitted or received, can be described on an orthonormal basis of two dimensions, I(n-phase) and Q(uadrature). Since phase is arctan(Q/I), random amplitude disturbances confined in either (or both) dimension, I and/or Q, cause continuously random phase errors. You can indeed think of noise as having two independent power spectra, one being a kind of AM in its nature (on instantaneous magnitude, or sqrt(I^2+Q^2)) and one PM in its nature (that arctan angle fluctuation). In some cases, the two are about equal in a power density sense. This is typical of Gaussian noise. But what gets measured in those "rig specification wars," is just the phase part alone since oscillator sources are pretty magnitude-constant in nature. So onward to phase noise!

 

* Signals can comprise continuous sequences of samples, as in DSP, or continuous voltages or currents as in analog (LCR networks and gain) electronics. But more and more, signals are discrete samples of a segmented, but otherwise continuous signal (think CW or phone), or else sequence of mathematically-defined symbols (think of what remains, from RTTY to PSK to packet systems like FT8). In digital signaling, a sufficient number of samples (satisfying the Nyquist criterion so as to avoid aliasing), and synchronized appropriately at a receiver, encompass a "baud" of the signal in ham speak (academics prefer "symbol"). In CW, it's a dit, a dah or a unit of carrier-free spacing. In phone signaling, it's way more complicated, due to the characteristics of ordinary speech. Just consider rig equalizers for a start. You could write a book on that subject alone, and speech algorithms in mobile, cellular systems expend thousands of manhours and many millions of dollars every year trying to improve on the status quo. We'll stop there for this page.

 

 

We cannot discuss phase without bowing first to time. Then we can get to phase.

 

Time, or in the case of transit time, delay, is a fundamental "quantity." Phase is not. It is derived from time.

Time is an SI unit. Phase is not even a "unit" (that would be a radian or a degree of angle, neither being an SI unit).

Phase is an arithmetic relationship between two closely-spaced observation instants, i.e. providing a measure of the elapsed time between two adjacent equal values of an "amplitude" of something, be that a signal or noise, or both.

Any observed (measured) specific instantaneous power level has a specific real-valued amplitude, for example the vertical deflection on a single oscilloscope trace. (This is taking a liberty with the idea of power, which is normally a statistic, an integral, not an instant value. If that statistic is the mean, or the sample average in practice, then that average value, translated into an amplitude, say, via Ohm's Law, might be a reasonable point at which to observe.) Now, take two most-closely-spaced such common-amplitude measures and we have the instantaneous period of the "power" that's being observed. This is a time difference. Divide that time difference by the period time of an idealized (mathematically perfect sinuousoid) center frequency fc; the resulting ratio could be a bit less than or a bit more than 1. That ratio multiplied by 2pi is the phase difference in radians. Take a bunch of such measurements and compute the mathematical variance (not the mean!) of the set, and you have the phase noise power.

Beyond this, we can combine any single instantaneous phase measure, made between two points of common amplitude, and we can express these two measures together as a complex number, or as a phasor. The common amplitude is a fraction of the maximum, and we call this the magnitude of the complex number. The phase is just the absolute value of 2pi x the ratio above minus 2pi. This is "2pi modulo" arithmetic. Because of periodicity, it makes little sense to ever talk about integer multiples of 2pi. See this link for a graphical illustration of all this.

Both signals and noise possess phase in this manner of differential measurement. In the case of a signal, phase becomes an interesting quantity as the measurement bandwidth shrinks to the "low pass" spectral width that, by definition, includes "most" of the signal. Uncertainty will always apply, but we can get a low error measure of phase by using good equipment and technique. This is one of several things that a high speed vector network analyzer, or VNA, can do. (The low speed, much less costly VNAs hams buy on the cheap give statistics of those phases and magnitudes, rather than a single-shot display that costs a lot of bucks.)

 

 

Apologies in advance. Phase noise forces us into considerations that run on and on.

Translated to a single frequency of interest, any random variation in a carrier's periodic transit time, or delay, between adjacent zero-crossings translates into an angular phase variation, or phase noise. This noise, all noise, is a random variable, or r.v. Added to an "ideal" signal, i.e. one with no randomness given the condition of no change in the information it bears in an instant, that now-corrupted signal now also becomes an r.v. And 90% of your communications theory course in first year grad school is all about recovering the (phase noise-free) information "underlying" this r.v.

The spectrum analyzer view at the preceeding link shows the spectrum of the phase noise on a (unmodulated) oscillator output, or simulation thereof by a direct digital synthesizer, which could be considered a carrier. The noise power is almost completely in the far left of the sweep, but "off of" the axis. Very little. This is a very clean source!

If you integrate the phase noise power density across the entire sweep, this is just 1/2 the total power of the source. (The other half is, by convention, the mirror image of these positive frequencies on the negative freq side of the vertical axis, never shown on specans but very definitely physically present.) You start describing that as the LO's power, almost ignoring all the power that is "well enough off of" fc Hz at the very left. This is the practical phase noise power.

Observable phase noise comes from various sources, usually just added together. In a simple communications link scenario, there is the phase noise from a modulation (or information) source, from a radio (or light) carrier source, and possibly then a process in the propagation path, then surely a receiver reference local oscillator (in the radio) or coherent detector or translator (in the case of light), and finally a demodulator (which contains the detector) back to raw information. Raw information is presumed to be phase noise free, even if it may contain information errors. Phase noise in the communications sense is an end-to-end transmission random-ness phenomenon. It has nothing to do with information, except that it commonly causes at least some finite error rate in digital transmission systems.

Because this is a complicated picture, most discussion about radio phase noise limits itself to a single key "specular" (or "single frequency," i.e. "pure," "clean") source that resides in a piece of radio equipment. This often, if not always, is a local oscillator (LO), one at the transmit end and a second one at the receive end. Usually just one LO per radio. In digital radios, the clock is derived from the same crystal reference as the RF LO(s) and so it all comes from one source. But in mixers, we do actually multiply two "phase processes" together to obtain a product.

With products, we must bring in the Fourier relationship of a product of two sinusoidal processes. Multiplying two sequences (as we will call these processes in the time domain) corresponds to convolving the Fourier transforms of the two sequences, over in the frequency domain. The convolution theorem is elementary in Fourier theory, appearing and proven in the first several chapters of a typical textbook, and it is a profound matter for radio transmission of low pass information-bearing signals. Since information (say, the audio spectrum of your voice) is always relatively very narrowband (compared to its transmitted propagation frequency), we usually just ignore the phase noise inherent in the information source (say a key, a microphone, a software converter of data ones and zeros, etc.). I.e., we take the information, or modulation (in radio) to be phase noise free for practical purposes. It isn't, of course, but its phase noise is very small compared to high frequency sources like LOs.

So it is by now clear that phase noise is a spectrum. When this is the spectrum of a modulated carrier, i.e. an information-bearing signal, the phase noise power density peaks at the center frequency (fc) of the single key specular source. And why is that? Simple. The probability distribution of the underlying mechanics of the noise r.v., e.g. for an LO being almost completely the thermal motion of atoms in a crystal, rolls off very fast with higher accelerations of the atoms. And so, lower accelerated, lower speed motions dominate, right down to (nearly) no motion at all. That point, of course, is the "pure," unadulterated carrier at precisely fc (which never exists because nothing is the universe is completely immobile!), but is, in practice, the integral of all the noisy energy within the measurement bandwidth (centered on fc) of whatever instrument you are using to look at the carrier. Nuf said!

So let's restate the above for more clarity in plain English. For an (unmodulated) LO, the phase noise so large at the LO source's exact center frequency (say, well within 1 Hz) as to be virtually undefined in power spectral density (PSD) in power units/Hz, falling off rapidly in PSD (in accordance with the source's internal attributes, such as the order of a PLL or a multiplier (say a diode followed by a filter) for carriers much above 100 MHz), all driven thermally, to often insignificant levels. You see -100dBc at "only" 30Hz offset in that image link above. On the other hand, in the case of a statistical or a wide bandwidth source, say the gaussian-distributed thermal noise from a resistor, phase noise is simply the angular part of the total PSD, becoming half the total power of "white noise," the other half being magnitude noise.

You cannot eliminate phase noise from any physical system. It is always there in the physics of any source, from DC to light. You can reduce it by reducing temperature. In theory, there is no phase noise at 0K; but no physical system can be at 0K! In practice, using materials that are more molecularly or atomically stable at a given temperature also reduces phase noise. This is the reason crystals are the common source for LOs of low phase noise. Crystals have very low real impedance at their fc, or very high Q by definition. (Of course, you can build an oscillator without a crystal, and it will have much lower Q and comparatively very substantial phase noise.)

It is important that phase noise not be confused with time jitter. The two are closely related, phase noise being a result of time jitter. Some web authors call phase noise "phase jitter," but this is a misnomer. A jitter is a step-like process, inherently abrupt. But phase noise is a continuum of random motion of an energy-bearing process, that often idealized as a sinuisoid, that both shifts (and hence distorts) the ideal process, that ideal thing being, e.g., a mathematically perfect sinusoidal wave expressed (for electrical circuits) in voltage or amperes. It is this continuum that makes the word "jitter" a poor descriptor of phase noise. Consider: If a phase modulation literally "steps" a carrier in phase, that's information, not noise!

Of course, phase noise is related to Q = f / (delta f). In a sense, the dimensionless value Q is integrated frequency, as weighted by a power spectrum, normalized to a center frequency, which is very much like a per-Hz amount of power normalized to total power, or the phase noise PSD evaluated at some selected point on the spectrum.

At the risk of redundancy, phase noise is well described as the intrinsic imperfection of a nominally "pure" tone, as from a crystal oscillator. Yes, a crystal oscillator has phase noise, primarily because it cannot oscillate, i.e. vibrate, at absolute zero temperature! Yet, crystals are still the king of solid state oscillators, right down to the transition to atomic clocks, which use vapors of rubidium and caesium atoms rather than crystals. (Just to add, atomic sources are based on electron orbital transitions, which are even less noisy than molecular or crystalline lattice thermal processes.) And so any received signal, even by a simple crystal detector, will contain that crystal's (or that of any reference's derived from a crystal, say via a PLL) phase noise. Thus, all digital clocks also.

Once we're in the realm of numbers, beyond D/A or A/D conversions, we are in phase-noise-free math. Caution: that doesn't mean we're in noise-free math! Just phase-noise-free math. Any raw data from a physical source, like an A/D converter, contains quantization noise. That propagates though any math. And any post-processing has its math representation limits built in, succumbing to round-off error noise. And going the other direction, across a D/A converter, we have the the quantization noise of the signal model, the phase noise of the conversion clock, etc., etc., just in the other direction. Yikes, it's noise all the way down, or all the way up. But noise of pure math can be made very small, let's just say negligible, compared with even the lowest physical phase noise, by using floating point processing. That was a reason for moving past integer processing, at some component cost. So we're done, for all practical purposes, adding noise at the point of the DSP manipulations. Whooray!

However, even digital electronic circuits must deal with clock phase noise to avoid a physical disaster called metastability, a bit beyond the topic to risk a pun. Fortunately, creating margins as set-up and hold times on register flip-flops, the likelihood of a metastability "event" (bit flip) decreases to approximately zero. Or else we wouldn't even have computers, let alone DSP radios. Whew!

From the above, you deduce that phase noise is an intrinsic aspect of any physical signal, from its creation onward. We can really only get rid of phase noise by starting and remaining in the world of pure mathematics. Unfortunately, so far at least, pure math cannot propagate! We need EM fields for that. So we are stuck with phase noise in all forms of radio, probably for good. We just have to make better and better sources to trim the problem down.

When a local oscillator (LO) is applied to a radio signal, in transmit or receive, the LO's phase noise is expressed across the entire bandwidth of the now-shifted (or perhaps detected) signal! This is an inescapable consequence of the Fourier relationship between multiplying in time and convolving in frequency. The phase noise shows up everywhere there is any signal energy! Cursed phase noise! But if it is small, really meaning a rapid rolloff from its central (at the nominal LO frequency) integrated power, which ought be almost all its power, aggregated into a bandwidth which is tiny compared with the information-bearing signal's bandwidth, then the phase power (vice the phase noise) of the "information process" will dominate it. A mouthful, yes, but rate of information actually is a power. This is good, that is until the signal in question is an undesired one, which is considered below, and is the very subject of reciprocal mixing dynamic range (RMDR) which we are seeing referred to all over in ham radio rig specifications trying to influence your rig purchasing decisions!

Phase noise is what we live with in all electromagnetic communications, all communications of any type using a reference frequency source. Now some communications, like laser, can be directly detected without a reference LO, and then other sources of noise become ascendant, like "shot noise" (at both the transmitter and receiver). (Note that there is still the phase noise of the modulator driving the laser!) Also, vacuum tube radios get much of their noise, again on both sides of the link, from cathode shot noise, which differs from phase noise and is another topic. Still, all these communications also see phase noise piled atop of everything from other parts of the channel, like the ionosphere for example. Phase noise is a trying thing in any technology.

For wideband signals, phase becomes a poor descriptor, and, pushing the limits, a complete failure to describe "channel phase noise." Here, the channel is everything from the digital modulator to the digital demodulator. In ham HF, we are always narrowband by reg. But at UHF and up, hams can use wideband signals, even spread spectrum, and must be aware of the primacy of time. That said, phase noise is becoming the epicenter of rig comparisons.

Modern rig design is caught-up in a love affair with low phase noise. And it's not completely disingenuous. For very low rate digital signals, the phase noise of the reference oscillators can be a big deal, even at high SNR. You don't put a 1 bps signal through a relatively broadband transponder (think a VHF relay station) and expect to get good coherent reception results, despite a 30dB SNR! You will not! You are phase noise-limited! So rig-to-rig, weak signal, really low rate modes like 6 bps FT8 and its ilk (worse yet is WSPR) are designed for noncoherent signaling using FSK, not PSK, discarding phase in favor of integrated power, or energy in a symbol bandwidth, that Eb/N number you see in WSPR receive reports. Note in dB: Eb/N = Eb/No - RefBW (say 2.8kHz). If the rigs are fantastic and the channel is very, very stable, then coherently-demodulated FSK, or CFSK, may be feasible, and that's about a 2dB gain for what it's worth. But any absolute precision of phase stability between random rigs at any particular moment in time is rendered moot by the random phase variations over one second (or so) of a typical HF channel.

Yet, modern rigs, for TX and RX, sport the best phase noise PSD they can reasonably get. Manufacturers make a big deal of it. There are two aspects to this. First is in receive, where, of primary interest, intermodulation of a nearby, very strong undesired signal with what there is of the receiver's own phase noise spectrum can result in an interfering noise product appearing at a desired signal's frequency. That can happen in any modulation mode from CW up. Second is in transmit, where low phase noise is partly about keeping a signal's bandwidth "tight," in the sense of a super high filter shape factor, especially when boosting the rig's transmit power well beyond what might be called a weak signal. The other part is about keeping the signal "coherent," in the sense of a coherent demodulator at the other end. In practical SSB phone, it will not matter much if voice power is tightly rolled off, even if from a pretty large vocal bandwidth! But it will matter at a receiver's decodable SNR limit for a very narrowband signal like FT8. It would be reasonable to say that the entire rig phase noise brouhaha is oriented to digital signals.

Beyond all this, one reason that very slow modulation symbol (baud) rates begin to fail on links of any SNR that are demodulated coherently, i.e. exploiting the received signal's phase, is because, taking WSPR as an example, a 0.45 bps signal suffers so significantly from just the transmitter's and the receiver's phase noise, a double aggravation, completely ignoring channel phase noise if the channel is stable over large fractions of a second. When integrating received symbol energy over such small bandwidths relative to radio frequency, meaning over such a relatively long time, that the lowest (closest-in to fo) phase noise begins to randomly cancel out part of its own energy. Then at some received channel SNR, whether weak or strong, doesn't even matter in that case. Even a strong, but sufficiently slow signal, has actually self-dissolved some of its own meaning!

 

 

So I seem to have promised some commentary on distortion.

Distortion is noise. That is, any received power that is not part of an accurate replica of the original information, e.g. a voice, etc., is noise, pure and simple.

But, unlike most of what nature throws at us, it need not be "random." It is generated from the same information you are desiring and seeking in the signal. But instead of a linear replica of that desired voice, key stroke, etc., you get some amount of the total received power subtracted from the desired power, and worse, added back in as bad stuff. Your ears can't decode it. This typically occurs as a result of a nonlinear process.

Nonlinearities abound in electronics, and even in radiating systems (...er, antennas).

The simplest nonlinearity most of us encounter as hams early in the game is the Class C amplifier. It turns sine waves into square waves! Worse, the same saturation mechanism inherent in Class C literally mixes all the square waves together. What a mess. It's often call a "forest of spurs." Remarkably, this is OK when the signal is one sine wave, because all such mixing at the fundamental frequency merely moves the phase of the amplified signal (the one we seek) around. It lands somewhere and stays there. And after product detection, say by BFO for CW, we can't hear those multitudinous components. It all just comes out as a CW tone of some arbitrary phase. With of course, some loss in strength as the higher (typically odd harmonic) components get filtered out the by amp's bandpass filter and even the antenna.

But don't expect that nice thing to happen with anything else! Phase in original information, e.g. a voice, etc., is the main thing! The central bias "carrier" in an AM signal may be spared distortion, but the sidebands are upheaved. Thus, the same happens with SSB. And anything else having information sidebands, FM, etc.

All this happens, to one degree or another, in a receiver as well. We often see specs on audio amplifiers that tout their low "total harmonic distortion," etc. That's what they're claiming you're mostly free of. But in a close pair of signals in the band you're using, you will encounter noticeable reciprocal mixing if the undesired one is effectively strong enough. That spec is the sometimes mysterious RMDR (DR for dynamic range). It indicates how strong a close undesired signal can be and still not bother you. Yes, there are numbers for all of this. But you get the idea.

Distortion is a huge topic for some purposes. No point going into all that here. Just know that's it's noise. And like the fairly random noise in your receiver's selected bandwidth, it's equally unavoidable. It just can be minimized to some degree by good filters, good design and, often, good luck.